Most people see a trigonometric function and instantly start to experience anxiety, either moderate or extreme. Primarily, this anxiety stems from lack of understanding. Let's start at the basics and work our way to a deeper understanding of the sine, cosine, and tangent functions.
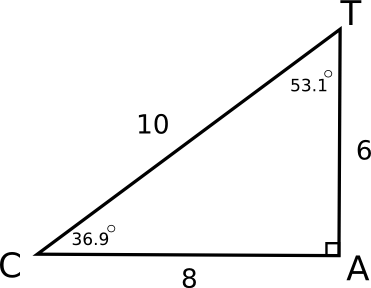
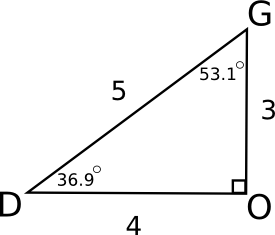
Trigonometric functions are basically comparing similar right triangles. Similar means that the triangles' angles are congruent (the same measure), and their side lengths are proportional. Look at the similar right triangles CAT and DOG. The fact that the triangles are proportional means that we can set up a proportion (equal ratios, or fractions) of corresponding parts. For example, side AT corresponds to side OG, and side CT corresponds to side DG. Here is the proportion that is important for understanding trigonometric functions.
These fractions are equal! This will always happen with similar triangles!
The main point is that we can pick any two sides of a triangle, make a ratio (fraction) out of the side lengths, and say that it is equal to the corresponding ratio from the other triangle. Here are two other proportions that we can set up. Again, when we evaluate the ratios, they are equal.
\frac{AT}{AC} = \frac{OG}{OD} |
\frac{CT}{CA} = \frac{DG}{DO} |
\frac{6}{8} = \frac{3}{4} |
\frac{10}{8} = \frac{5}{4} |
If you know that triangles are similar, you can find out missing side lengths if you know only one of the three side lengths. For example, let's look at triangle MUT and compare it to triangle DOG.
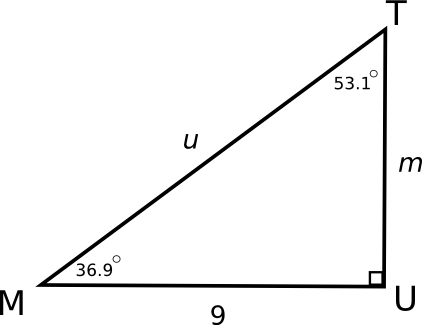

Because triangle MUT is similar to triangle DOG, side UT corresponds to side OG,side MU corresponds to side DO, and side MT corresponds to side DG. We can set up three different proportions of corresponding parts.
\frac{UT}{MT} = \frac{OG}{DG} \ |
\frac{UT}{MU} = \frac{OG}{DO} \
| \frac{MU}{MT} = \frac{DO}{DG} |
\frac{m}{u} = \frac{3}{5} |
\frac{m}{9} = \frac{3}{4} |
\frac{9}{u} = \frac{4}{5} |
We could cross multiply to solve for the variables, thus finding the lengths of unknown side lengths u and m.
4 \cdot m=9\cdot 3 |
9 \cdot 5=4 \cdot u | |
4 \cdot m=27 |
45=4 \cdot u | |
m= \frac{27}{4} |
\frac{45}{4}=u | |
m= 6 \frac{3}{4} |
\frac{1}{4}=u |
Now we know everthing that there is to know about the triangle MUT.
Any triangle with the angles measureing 36.9 ^\circ, 53.1 ^\circ , and 90 ^\circ will always have ratios of side lengths that reduce to \frac{3}{5}, \frac{3}{4}, and \frac{4}{5} . The idea that similar figures always have equal ratios gave birth to the idea behind trigonometric functions. Since there are three ratios for every right triangle, there are three trigonometric functions. (Technically, we can take the reciprocals of the ratios, which makes it six ratios total. But, it is redundant and isn't important yet. Basically, this is where the sec, tan, and csc trigonometric functions come from.)
In order to distinguish between the three different ratios, we have to be able to look at any triangle and specify which two side lengths we should use to make our ratio. To do this, each side of the right triangle is called either opposite, adjacent, or the hypotenuse, depending on which angle we will focus on.
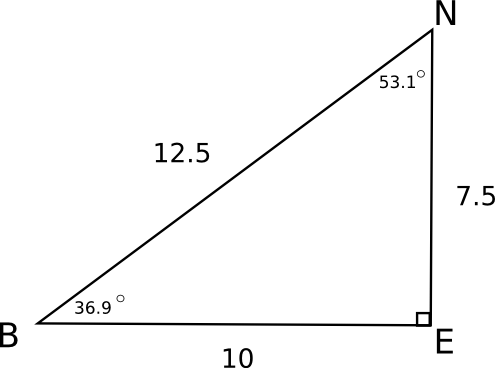
In triangle BEN, we are first going to focus on \angle B.
Side EN is opposite \angle B.
Side BE is adjacent to \angle B.
The hypotenuse of the triangle is side BN.
But, if we focus on \angle N, the relationship to the sides changes.
Side BE is opposite \angle N.
Side EN is adjacent to \angle N.
The hypotenuse of the triangle is still side BN.
We won't focus on the 90^\circ angle because trigonometric functions are defined by right triangles. The fact that there is a 90^\circ does not give us any additional information. Whereas we could compute the third angle if we are told that we have a right triangle that also has an angle of some specified measurement in degrees, such as \angle B and \angle N.
The angle we use and which trigonometric function we use tells us which side lengths we need to make the trigonometric ratio.
Here are the definitions of the trigonometric functions.
| sine of an angle = \frac{opposite}{hypotenuse} |
| cosine of an angle = \frac{adjacent}{hypotenuse} |
| tangent of an angle = \frac{opposite}{adjacent} |
Let's find all of the trigonometric ratios for the triangle BEN.

| sin(B) = \frac{opposite \angle B}{hypotenuse} = \frac{7.5}{12.5} = 0.6 = \frac{3}{5} |
| cos(B) = \frac{adjacent \angle B}{hypotenuse} = \frac{10}{12.5} = 0.8 = \frac{4}{5} |
| tan(B) = \frac{opposite \angle B}{adjacent \angle B} = \frac{7.5}{10} = 0.75 = \frac{3}{4} |
Notice that the ratios are \frac{3}{5}, \frac{4}{5}, and \frac{3}{4} as we predicted would happen. Also notice that if you evaluate sin(36.9^\circ) with a calulator you get 0.6004. Similarly, cos(36.9^\circ)= 0.7997 and tan(36.9^\circ) = 0.7508.
Similarly, we can evaluate the trigonometric functions with respect to \angle N.
| sin(N) = \frac{10}{12.5} = 0.8 = \frac{4}{5} |
| cos(N) = \frac{7.5}{12.5} = 0.6 = \frac{3}{5} |
| tan(N) = \frac{10}{7.5} = 1.3 = \frac{4}{3} |
All of the examples we have looked at are similar triangles with 36.9^\circ, 53.1^\circ , and 90^\circ angles. The same idea works with any right triangle you might have. Think of trigonometric ratios as a huge list of ratios of every possible right triangle you can come up with. Some textbooks even have a list of the trigonometric ratios for all of the angles ranging from 0^\circ to 90^\circ.